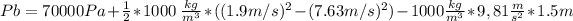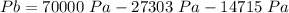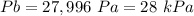Question

Water flows through a pipe of 100 mm at the rate of 0.9 m3 per minute at section A. It tapers to 50mm diameter at B, A being 1.5 m above B. The pressure in the pipe at A is 70 kPa above atmospheric. Assuming no loss of energy between A and B, determine, a)- the velocity of A and B b)- Find pressure at B

Answer 1

The velocities in points A and B are 1.9 and 7.63 m/s respectively. The Pressure at point B is 28 Kpa.

Step-by-step explanation:

Assuming the fluid to be incompressible we can apply for the continuity equation for fluids:

`Aa.Va=Ab.Vb=Q`

Where A, V and Q are the areas, velocities and volume rate respectively. For section A and B the areas are:

`Aa=(pi.Da^2)/(4)= (\pi.(0.1m)^2)/(4)=7.85*10^(-3)\ m^3`

`Ab=(pi.Db^2)/(4)= (\pi.(0.05m)^2)/(4)=1.95*10^(-3)\ m^3`

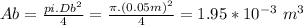
Using the volume rate:

`Va=(Q)/(Aa)=(0.9m^3)/(7.85*10^(-3)\ m^3) = 1.9\ m/s`

`Vb = (Q)/(Ab)= (0.9m^3)/(1.96*10^(-3)\ m^3) = 7.63\ m/s`

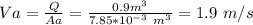
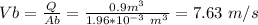
Assuming no losses, the energy equation for fluids can be written as:

`Pa+(1)/(2)pa.Va^2+pa.g.za=Pb+(1)/(2)pb.Vb^2+pb.g.zb`

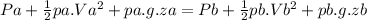
Here P, V, p, z and g represent the pressure, velocities, height and gravity acceleration. Considering the zero height level at point A and solving for Pb:

`Pb=Pa+(1)/(2)pa(Va^2-Vb^2)-pa.g.za`

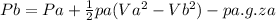
Knowing the manometric pressure in point A of 70kPa, the height at point B of 1.5 meters, the density of water of 1000 kg/m^3 and the velocities calculated, the pressure at B results:

`Pb = 70000Pa+ (1)/(2)*1000\ (kg)/(m^3)*((1.9m/s)^2 - (7.63m/s)^2) - 1000(kg)/(m^3)*9,81(m)/(s^2)*1.5m`

`Pb = 70000\ Pa-27303\ Pa - 14715\ Pa`

`Pb = 27,996\ Pa = 28\ kPa`