Answer:
The concentration of a saturated solution of CuF₂ in aqueous 0.20 M NaF is 4.0×10⁻⁵ M.
Step-by-step explanation:
Consider the ICE take for the solubility of the solid, CuF₂ as:
CuF₂ ⇄ Cu²⁺ + 2F⁻
At t=0 x - -
At t =equilibrium (x-s) s 2s
The expression for Solubility product for CuF₂ is:
![K_(sp)=\left [ Cu^(2+) \right ]\left [ F^- \right ]^2](https://img.qammunity.org/2020/formulas/chemistry/college/q7jz3wkcljxjzf5jgj9j49oe8qz8iex3eh.png)
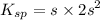
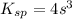
Given s = 7.4×10⁻³ M
So, Ksp is:
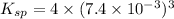
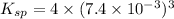
Ksp = 1.6209×10⁻⁶
Now, we have to calculate the solubility of CuF₂ in NaF.
Thus, NaF already contain 0.20 M F⁻ ions
Consider the ICE take for the solubility of the solid, CuF₂ in NaFas:
CuF₂ ⇄ Cu²⁺ + 2F⁻
At t=0 x - 0.20
At t =equilibrium (x-s') s' 0.20+2s'
The expression for Solubility product for CuF₂ is:
![K_(sp)=\left [ Cu^(2+) \right ]\left [ F^- \right ]^2](https://img.qammunity.org/2020/formulas/chemistry/college/q7jz3wkcljxjzf5jgj9j49oe8qz8iex3eh.png)
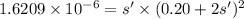
Solving for s', we get
s' = 4.0×10⁻⁵ M
The concentration of a saturated solution of CuF₂ in aqueous 0.20 M NaF is 4.0×10⁻⁵ M.