Question

How much work is done lifting a 12-m chain that is initially coiled on the ground and has a density 2 kg/m so that its top end is 8 m above the ground? (Assume that acceleration due to gravity is g = 9.8 m/s2.)

Answer 1

W = 627.2 J

Step-by-step explanation:

Given:

`\rho_(chain)` = 2kg/m

length of chain = 12 m

length pulled will be = 8 m

We know

Work done (W) = mgh

where

m = mass of the object

g= acceleration due to gravity

h = displacement

For a small length dy of the chain, the work done can be written as:

dW = (mass of the small length pulled)× g×dy

dW = 2kg/m ×dy×9.8×y

where, y is the distance from the ground level of the end of chain

integerating the above equation

W =
`\int\limits^8_0 {19.6y} \, dx`

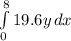
W =
`[19.6(y^2)/(2)]_(0)^(8)`

W = 627.2 J