Let
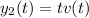 . Then
. Then
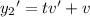
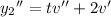
and substituting these into the ODE gives
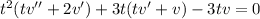
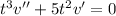
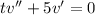
Let
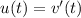 , so that
, so that
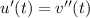 . Then the ODE is linear in
. Then the ODE is linear in
 , with
, with
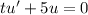
Multiply both sides by
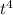 , so that the left side can be condensed as the derivative of a product:
, so that the left side can be condensed as the derivative of a product:
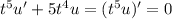
Integrating both sides and solving for
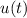 gives
gives
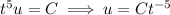
Integrate again to solve for
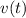 :
:
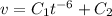
and finally, solve for
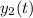 by multiplying both sides by
by multiplying both sides by
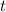 :
:
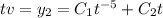
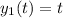 already accounts for the
already accounts for the
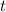 term in this solution, so the other independent solution is
term in this solution, so the other independent solution is
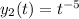 .
.