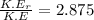Answer:
Step-by-step explanation:
Given:
mass, m = 87.5kg
Velocity, V = 0.900c
now,
the relativistic kinetic energy id given as:
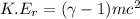 ...........(1)
...........(1)
where,
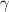 = relativistic factor, given as;
= relativistic factor, given as;
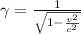
Now, the classical kinetic energy is given as:
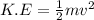 ..........(2)
..........(2)
Dividing the equation (1) by (2) we get
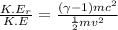
or
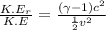
substituting the values in the equation we get,
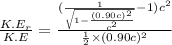
or