Question

Use Gauss' law to find the E field of an infinite solid cylinder of charge of radius R and charge density lambda per unit length. As usual, draw everything on the diagrams and label them.

Answer 1

`E = (\lambda)/(2\pi \epsilon_0 r)`

Step-by-step explanation:

As we know that electric field due to long cylinder on a cylindrical Gaussian surface must be constant

so on the Gaussian surface we will have

`\int E. dA = (q_(en))/(\epsilon_0)`

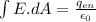
now the electric field is passing normally through curved surface area of the cylinder

so we will have

`E (2\pi rL) = (q_(en))/(\epsilon_0)`

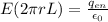
here enclosed charge in the cylinder is given as

`q_(en) = \lambda L`

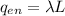
from above equation

`E(2\pi rL) = (\lambda L)/(\epsilon_0)`

`E = (\lambda)/(2\pi \epsilon_0 r)`