Answer:
Total distance D=7.66 ft
Explanation:
Given that:
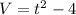
Here velocity of particle will be zero at t=2 sec,so we take interval to find total distance.
We know that
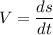
ds=V dt
So
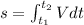
It means that ,the area of velocity-time(V-t) graph will give the displacement.
Given that
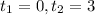
So now by putting the value in above integration
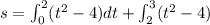
![s=\left [(1)/(3)t^3-4t\right ]_o^2+\left [(1)/(3)t^3-4t\right]_2^3](https://img.qammunity.org/2020/formulas/physics/college/4uip1ipwpsk0xbbkf6jawp4h8mu1a90xzp.png)
s= -5.33+2.33 ft
s= -3 ft (we know that displacement is a vector quantity so it have sing)
So this is the displacement of particle at time 0 sec to 3 sec.
To find the total distance we will add all take mode on -5.33 ft and and will add with 2.33 ft instead of subtract.
So the total distance travelled by particle D=7.66 ft.
D=7.66 ft