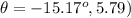Answer:
point of horizontal tangent is
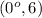 and point of vertical tangent is
and point of vertical tangent is
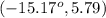
Explanation:
For a horizontal tangent it's slope should be zero thus
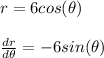
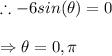
Thus the ordered pair of
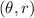 becomes (0,6) at this point tangent is horizontal
becomes (0,6) at this point tangent is horizontal
For a vertical tangent it's slope should be

Again differentiating the given curve we get
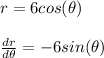
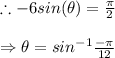
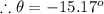
Thus the ordered pair of vertical tangent becomes (