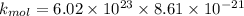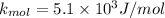Answer:
a)
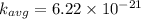
b)
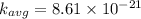
c)
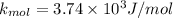
d)
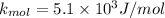
Step-by-step explanation:
Average translation kinetic energy (
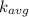 ) is given as
) is given as
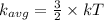 ....................(1)
....................(1)
where,
k = Boltzmann's constant ; 1.38 × 10⁻²³ J/K
T = Temperature in kelvin
a) at T = 27.8° C
or
T = 27.8 + 273 = 300.8 K
substituting the value of temperature in the equation (1)
we have
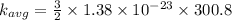
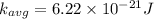
b) at T = 143° C
or
T = 143 + 273 = 416 K
substituting the value of temperature in the equation (1)
we have
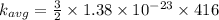
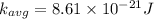
c ) The translational kinetic energy per mole of an ideal gas is given as:
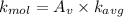
here
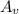 = Avagadro's number; ( 6.02×10²³ )
= Avagadro's number; ( 6.02×10²³ )
now at T = 27.8° C
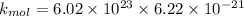
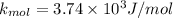
d) now at T = 143° C