Question

Triangle ABC has coordinates A (0, 1) B (0, 2) and C (3,2). If Triangle ABC is equivalent to triangle EDF, what is the measure of DF?

3
3.2
4
4.4

Answer 1

DF = 3

Explanation:

If ABC is equivalent to EDF, then DF is equivalent to BC, which form the following ordered pairs:

D = (0,2)

F = (3,2)

It can be seen that both pairs have the same value of "y" or second value, that is 2.

As a rule, when the points are located on the y-axis (of the ordinates) or on a line parallel to this axis, the distance between the points corresponds to the absolute value of the difference of their ordinates.

So,

DF = D(x) + F(x) = 0 + 3 = 3

If we apply the equation of the distance between two points we get the same result,

`DF=\sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)   }=\sqrt{(3-0)^(2)+(2-2)^(2)   }=\sqrt{(3)^(2)+(0)^(2)   }=√(9+0   )=√(9)=3`

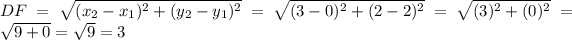
Hope this helps!

Answer 2

3

Explanation:

Segment BC corresponds to segment DF. The length of BC is the distance between coordinates (0, 2) and (3, 2). These points are on the same horizontal line (y=2), so the distance between them is the difference of their x-coordinates: 3 - 0 = 3.