Question

The probability that a part produced by a certain? factory's assembly line will be defective is 0.035. Find the probabilities that in a run of 44 ?items, the following results are obtained. ?(a) Exactly 3 defective items ?(b) No defective items ?(c) At least 1 defective item

Answer 1

Explanation:

P\left ( defective item\right )=0.035

Using binomial distribution

Where p= probability of success

q=probability of failure

Here p=0.035

q=1-0.035=0.965

`^nC_(r)P^(r)q^(n-r)`

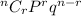
(i)for exactly 3 defective items i.e. r=3

P
`\left ( r=3\right )`=
`^(44)C_(3)`
`\left ( 0.035\right )^(3)\left ( 0.965\right )^(44-3)`

P=
`(44!)/(41!3!)* \left ( 0.035\right )^3\left ( 0.965\right )^(41)`

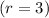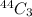
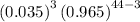
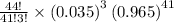
P=0.1317

(ii)No defective item i.e. r=0

P
`\left ( r=0\right )`=
`^(44)C_(0)`
`\left ( 0.035\right )^(0)`
`\left ( 0.965\right )^(44-0)`

P=
`(44!)/(44!0!)* \left ( 0.035\right )^0\left ( 0.965\right )^(44)`

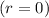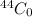
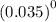
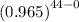
P=0.2085

(iii)At least 1 defective item

P=1-P(zero defective item)

P=1-
`^(44)C_(1)\left ( 0.035\right )^(1)\left ( 0.965\right )^(44-1)`

P=1-
`(44!)/(43!1!)* \left ( 0.035\right )^1`
`\left ( 0.965\right )^(43)`

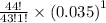
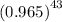
P=0.6671