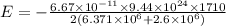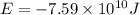Given:
mass of satellite, m = 1710 kg
altitude, h =
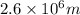
G =
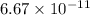
we know
mass of earth,
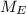 =
=
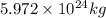
Here, according to question we will consider
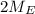 =
=

radius of earth,
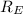 =
=

Formulae Used and replacing
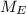 by
by
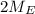 :
:
1).

2).
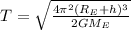
3).

4).
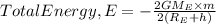
where,
v = orbital velocity of satellite
T = time period
KE = kinetic energy
Solution:
Now, Using Formula (1), for orbital velocity:
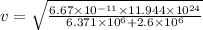
v =
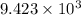 m/s
m/s
Using Formula (2) for time period:
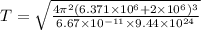

Now, Using Formula(3) for kinetic energy:
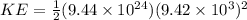

Now, Using Formula(4) for Total energy: