Question

The owner of a fabric store has determined that the profits P of the store are approximately given by P(x) = -x^2 + 70x+67, where x is the yards of fabric sold daily. Find the maximum profit to the nearest dollar. a) $617 b) $792 c) $1017 d) $1292 e) none

Answer 1

Answer: Option 'd' is correct.

Explanation:

Since we have given that

Profit function of the store is given by

`P(x)=-x^2+70x+67`

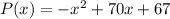
We need to find the maximum profit.

For this, we first derivate the above function:

`P'(x)=-2x+70`

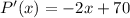
Now, put P(x) = 0, we get that

`-2x+70=0\\\\-2x=-70\\\\x=35`

Now, we will check that its maximality by finding the second derivative:

`P''(x)=-2<0`

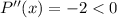
it gives maximum profit at x = 35 yards.

And the maximum profit would be

`P(35)=-(35)^2+70* 35+67=\$1292`

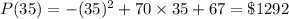
Hence, Option 'd' is correct.