Answer:
Poission Ratio = 0.2784
Explanation:
we know that
Poission ratio is defined as
μ =

We also know that lateral strain =
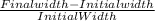
In our case
Final width = 2.89945 in
Initial width = 2.9 in (Area of cross section (width x depth) = 2.9 in x 2.9 in)
Thus lateral strain =
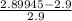
Lateral strain =
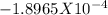
Similarly longitudinal strain =

Thus longitudinal strain =
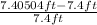
Longitudinal strain =

Thus by formula poission ratio =
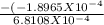
Poission Ratio = 0.2784