Answer:
The correct option is 4.
Explanation:
It is given that the rate of recipt of income from the sales of vases from 1988 to 1993 can be approximated by
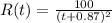
billion dollars per year, where t is time in years since January 1988.
We need to estimate the total change in income from January 1988 to January 1993.
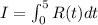
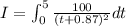
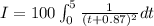
On integration we get
![I=-100[(1)/((t+0.87))]_(0)^(5)](https://img.qammunity.org/2020/formulas/mathematics/college/f947idsnnvoa6ljrgxsg4enj8y7x0zfpgk.png)

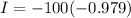
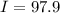
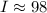
The total change in income from January 1988 to January 1993 is $98. Therefore the correct option is 4.