Question

Two point charges are on the y-axis. A 3.0 µC charge is located at y = 1.15 cm, and a -2.28 µC charge is located at y = -2.00 cm. (a) Find the total electric potential at the origin. g

Answer 1

Total electric potential,
`V=1.32* 10^6\ volts`

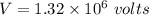
Step-by-step explanation:

It is given that,

First charge,
`q_1=3\ \mu C=3* 10^(-6)\ C`

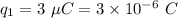
Second charge,
`q_2=-2.28\ \mu C=-2.28* 10^(-6)\ C`

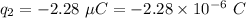
Distance of first charge from origin,
`r_1=1.15\ cm=0.0115\ m`

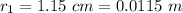
Distance of second charge from origin,
`r_2=2\ cm=0.02\ m`

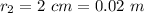
We need to find the total electric potential at the origin. The electric potential at the origin is given by :

`V=(kq_1)/(r_1)+(kq_2)/(r_2)`

`V=k((q_1)/(r_1)+(q_2)/(r_2))`

`V=9* 10^9((3* 10^(-6))/(0.0115)+(-2.28* 10^(-6))/(0.02))`

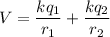
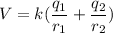
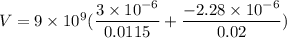
V = 1321826.08 V

or

`V=1.32* 10^6\ volts`

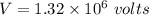
So, the total electric potential at the origin is
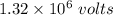`1.32* 10^6\ volts`. Hence, this is the required solution.