Question

The force between two electrical charges is 0.3 N. What would be the force if the charges are doubled, and the distance between them increased by 100%?

(Please show clear steps/explanation)

Answer 1

The new force F' will be same of the original force F.

Step-by-step explanation:

Given that,

Charges = 0.3

We need to calculate the force between the charges

Suppose that the distance between the charges is r.

The force between the charges

`F =(kq_(1)q_(2))/(r^2)`

Put the value into the formula

`F=(k*0.3*0.3)/(r^2)`

`F=(k*(0.09))/(r^2)`

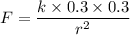
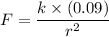
If the charges are doubled, and the distance between them increased by 100%.

So, The charges are 0.6 and the distance is 2r.

Then,

The force between the charges

`F'=(k*0.6*0.6)/((2r)^2)`

`F'=(k*0.09)/(r^2)`

`F'=F`

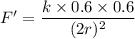
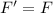
Hence, The new force F' will be same of the original force F.