Question

Two objects that may be considered point masses are initially separated by a distance d. The separation distance is then decreased to d/4. How does the gravitational force between these two objects change as a result of the decrease?

Answer 1

Increased by 16 times

Step-by-step explanation:

F = Gravitational force between two bodies

G = Gravitational constant = 6.67408 × 10⁻¹¹ m³/kg s²

m₁ = Mass of one body

m₂ = Mass of other body

d = distance between the two bodies

`F=(Gm_1m_2)/(d^2)\\ F=(1)/(d^2)\quad \text {(as G and masses are constant)}`

`F_(new)=(1)/(\left ((d)/(4)\right )^2)\\\Rightarrow F_(new)=(1)/((d^2)/(16))\\\Rightarrow F_(new)={16}* (1)/(d^2)\\\Rightarrow F_(new)=16* F`

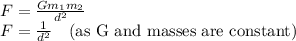
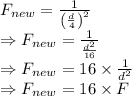
∴Force will increase 16 times