Question

g A projectile is launched with speed v0 from point A. Determine the launch angle ! which results in the maximum range R up the incline of angle " (where 0 ≤ " ≤ 90°). Evaluate your results for " = 0, 30°, and 45°

Answer 1

The launch angle that results in the maximum range of a projectile up an incline depends on the initial speed and the angle of the incline. For conditions neglecting air resistance, the maximum range is obtained at 45 degrees. If air resistance is considered, the maximum angle is around 38 degrees.

Step-by-step explanation:

The range of a projectile launched up an incline depends on the launch angle. To determine the launch angle that results in the maximum range, we need to consider the initial speed and the angle of the incline. Figure 3.38(b) shows that for a fixed initial speed, the maximum range is obtained at 45 degrees. However, this is only true for conditions neglecting air resistance. If air resistance is considered, the maximum angle is around 38 degrees. It is also interesting to note that for every initial angle except 45 degrees, there are two angles that give the same range, and the sum of those angles is 90 degrees.

Answer 2

The range is maximum when the angle of projection is 45 degree.

Step-by-step explanation:

The formula for the horizontal range of the projectile is given by

`R = (u^(2)Sin2\theta )/(g)`

The range should be maximum if the value of Sin2θ is maximum.

The maximum value of Sin2θ is 1.

It means 2θ = 90

θ = 45

Thus, the range is maximum when the angle of projection is 45 degree.

If the angle of projection is 0 degree

R = 0

It means the horizontal distance covered by the projectile is zero, it can move in vertical direction.

If the angle of projection is 30 degree.

`R = (u^(2)Sin60 )/(9.8)`

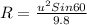
R = 0.088u^2

If the angle of projection is 45 degree.

`R = (u^(2)Sin90 )/(g)`

R = u^2 / g