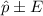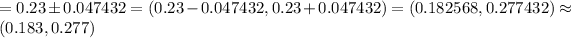Answer: (0.183,0.277)
Explanation:
Given : Out of 300 people sampled, 69 preferred Candidate A.
Sample size : n= 300
Proportion of people proffered Candidate A :

Significance level :
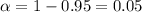
Standard error :
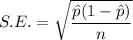
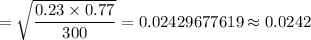
Margin of error :
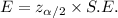
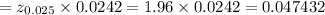
The confidence interval for the population proportion is given by :-