Explanation:
Given:
Let triangle ACD is aright angle triangle with right angle at C. A line perpendicular to AB join C.
Therefore we can say that line segment CD divides angle at C into two equal angles.
So in ΔACD and ΔCDB
∠ ACD = ∠DCB
and ∠ADC = ∠BDC = 90°
and CD =CD
∴ we can say that ΔACD and ΔCDB are similar triangles.
∴ Area of ΔACD =
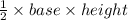
=
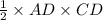
Area of ΔCDB =
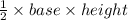
=

Therefore ratio of the areas of ΔACD and ΔCDB is
i.e.
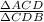 =
=
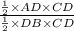
=
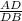
∴ Area of the ratio of
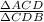 =
=
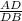
Hence proved