Question

A charge q = 3 × 10-6 C of mass m = 2 × 10-6 kg, and speed v = 5 × 106 m/s enters a uniform magnetic field. The mass experiences an acceleration a = 3 × 104 m/s2. What is the minimum magnetic field that would produce such an acceleration?

Answer 1

Magnetic field, B = 0.004 mT

Step-by-step explanation:

It is given that,

Charge,
`q=3* 10^(-6)\ C`

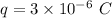
Mass of charge particle,
`m=2* 10^(-6)\ C`

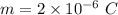
Speed,
`v=5* 10^(6)\ m/s`

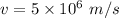
Acceleration,
`a=3* 10^(4)\ m/s^2`

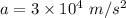
We need to find the minimum magnetic field that would produce such an acceleration. So,

`ma=qvB\ sin\theta`

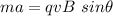
For minimum magnetic field,

`ma=qvB`

`B=(ma)/(qv)`

`B=(2* 10^(-6)\ C* 3* 10^(4)\ m/s^2)/(3* 10^(-6)\ C* 5* 10^(6)\ m/s)`

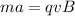
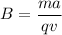
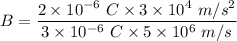
B = 0.004 T

or

B = 4 mT

So, the magnetic field produce such an acceleration at 4 mT. Hence, this is the required solution.