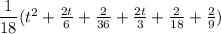Question

Solve the following ODE's: c) y* - 9y' + 18y = t^2

Answer 1

y =
`C_1e^(3t)+C_2e^(6t)` +
`(1)/(18)(t^2+(2t)/(6) + (2)/(36)+(2t)/(3)+(2)/(18)+(2)/(9))`

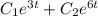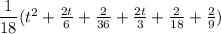
Explanation:

y''- 9 y' + 18 y = t²

solution of ordinary differential equation

using characteristics equation

m² - 9 m + 18 = 0

m² - 3 m - 6 m+ 18 = 0

(m-3)(m-6) = 0

m = 3,6

C.F. =
`C_1e^(3t)+C_2e^(6t)`

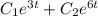
now calculating P.I.

`P.I. = (t^2)/(D^2 - 9D +18)`

`P.I. = (t^2)/((D-3)(D-6))\\P.I. =(1)/(18)(1-(D)/(3))^(-1)(1-(D)/(6))^(-1)(t^2)\\P.I. =(1)/(18)(1-(D)/(3))^(-1)(1+(D)/(6)+(D^2)/(36)+....)(t^2)\\P.I. =(1)/(18)(1-(D)/(3))^(-1)(t^2+(2t)/(6) + (2)/(36))\\P.I. =(1)/(18)(1+(D)/(3)+(D^2)/(9)+....)(t^2+(2t)/(6) + (2)/(36))\\P.I. =(1)/(18)(t^2+(2t)/(6) + (2)/(36)+(2t)/(3)+(2)/(18)+(2)/(9))`

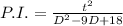
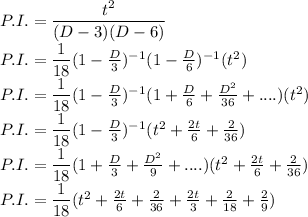
hence the complete solution

y = C.F. + P.I.

y =
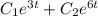`C_1e^(3t)+C_2e^(6t)` +
`(1)/(18)(t^2+(2t)/(6) + (2)/(36)+(2t)/(3)+(2)/(18)+(2)/(9))`