Question

A uniform solid sphere of radius r = 0.490 m and mass m = 13.5 kg turns counterclockwise about a vertical axis through its center (when viewed from above). Find its vector angular momentum about this axis when its angular speed is 2.9 rad/s.

Answer 1

Vector angular momentum about this axis of the sphere is:

L= 3.76
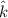`\hat k` kg-m²/sec

Step-by-step explanation:

The formula for the moment of inertia of a sphere is:

`I=(2)/(5)* MR^2`

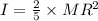
Given:

Mass of the sphere = 13.5 kg

Radius of the sphere = 0.490 m

Thus, moment of inertia :

`I=(2)/(5)* 13.5* (0.490)^2 kg\ m^2`

`I=1.29654 kg\ m^2`

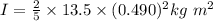
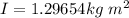
The expression for the angular momentum is:

L=I×ω

Given:

Angular speed(ω) = 2.9 rad/s

I, above calculated = 1.29654 kgm⁻²

Thus, angular momentum is:

L= 1.29654×2.9 kg-m²/sec

L= 3.76 kg-m²/sec

Given, the sphere is turning counterclockwise about the vertical axis. Thus, the direction of the angular momentum will be on the upper side of the plane. (
`+\hat k` ).

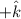Thus, angular momentum with direction is:

L= 3.76
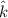`\hat k` kg-m²/sec