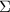 should have parameterization
should have parameterization
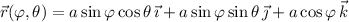
if it's supposed to capture the sphere of radius
 centered at the origin. (
centered at the origin. (
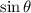 is missing from the second component)
is missing from the second component)
a. You should substitute
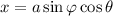 (missing
(missing
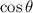 this time...). Then
this time...). Then
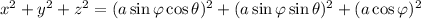
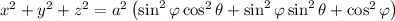
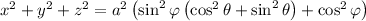
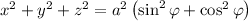
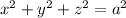
as required.
b. We have
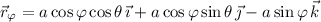
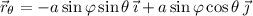
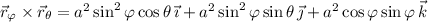
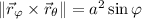
c. The surface area of
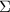 is
is
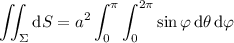
You don't need a substitution to compute this. The integration limits are constant, so you can separate the variables to get two integrals. You'd end up with
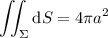
# # #
Looks like there's an altogether different question being asked now. Parameterize
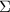 by
by
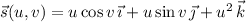
with
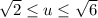 and
and
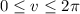 . Then
. Then
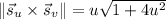
The surface area of
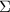 is
is
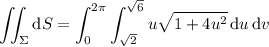
The integrand doesn't depend on
 , so integration with respect to
, so integration with respect to
 contributes a factor of
contributes a factor of
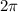 . Substitute
. Substitute
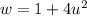 to get
to get
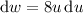 . Then
. Then
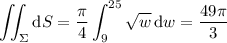
# # #
Looks like yet another different question. No figure was included in your post, so I'll assume the normal vector points outward from the surface, away from the origin.
Parameterize
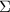 by
by
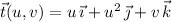
with
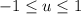 and
and
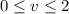 . Take the normal vector to
. Take the normal vector to
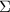 to be
to be
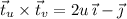
Then the flux of
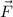 across
across
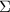 is
is
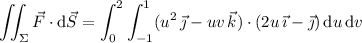
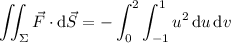
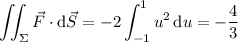
If instead the direction is toward the origin, the flux would be positive.