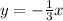Question

What is the equation of the following line? (-3, 1) and (0,0)

Answer 1

`y = -(1)/(3)x`

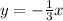
Explanation:

The equation of a line in the pending intersection is:

`y = mx + b`

Where m is the slope of the line and b is the intercept with the y axis.

If we know two points
`(x_1, y_1)` and
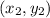`(x_2, y_2)` then we can find the equation of the line that passes through those points.

`m =(y_2-y_1)/(x_2-x_1)`

`b=y_1-mx_1`

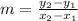
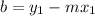
In this case the points are (-3, 1) and (0,0)

Therefore

`m =(0-1)/(0-(-3))`

`m =(-1)/(3)`

`b=1-((-1)/(3))(-3)`

`b=0`

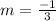
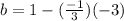
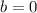
Finally the equation is:

`y = -(1)/(3)x`

Answer 2

`y = -(1)/(3) x`

Explanation:

We are given the following two points and we are to find the equation of the line which passes through them:

(-3, 1) and (0,0)

Slope =
`(0-1)/(0-(-3)) =-(1)/(3)`

Substituting the given values and the slope in the standard form of the equation of a line to find the y intercept:

`y=mx+c`

`0=-(1)/(3) (0)+c`

`c=0`

So the equation of the line is
`y = -(1)/(3) x`