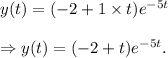Question

Solve y'' + 10y' + 25y = 0, y(0) = -2, y'(0) = 11 y(t) = Preview

Answer 1

Answer: The required solution is

`y=(-2+t)e^(-5t).`

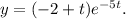
Step-by-step explanation: We are given to solve the following differential equation :

`y^(\prime\prime)+10y^\prime+25y=0,~~~~~~~y(0)=-2,~~y^\prime(0)=11~~~~~~~~~~~~~~~~~~~~~~~~(i)`

Let us consider that

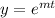`y=e^(mt)` be an auxiliary solution of equation (i).

Then, we have

`y^prime=me^(mt),~~~~~y^(\prime\prime)=m^2e^(mt).`

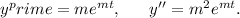
Substituting these values in equation (i), we get

`m^2e^(mt)+10me^(mt)+25e^(mt)=0\\\\\Rightarrow (m^2+10y+25)e^(mt)=0\\\\\Rightarrow m^2+10m+25=0~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~[\textup{since }e^(mt)\\eq0]\\\\\Rightarrow m^2+2* m*5+5^2=0\\\\\Rightarrow (m+5)^2=0\\\\\Rightarrow m=-5,-5.`

So, the general solution of the given equation is

`y(t)=(A+Bt)e^(-5t).`

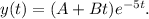
Differentiating with respect to t, we get

`y^\prime(t)=-5e^(-5t)(A+Bt)+Be^(-5t).`

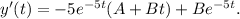
According to the given conditions, we have

`y(0)=-2\\\\\Rightarrow A=-2`

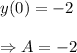
and

`y^\prime(0)=11\\\\\Rightarrow -5(A+B*0)+B=11\\\\\Rightarrow -5A+B=11\\\\\Rightarrow (-5)*(-2)+B=11\\\\\Rightarrow 10+B=11\\\\\Rightarrow B=11-10\\\\\Rightarrow B=1.`

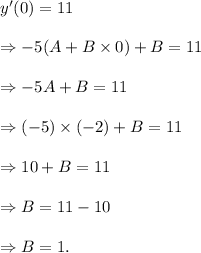
Thus, the required solution is

`y(t)=(-2+1* t)e^(-5t)\\\\\Rightarrow y(t)=(-2+t)e^(-5t).`