a. The moduli are coprime, so you can apply the Chinese remainder theorem directly. Let
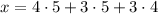
- Taken mod 3, the last two terms vanish, and
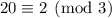 so we need to multiply by the inverse of 2 modulo 3 to end up with a remainder of 1. Since
so we need to multiply by the inverse of 2 modulo 3 to end up with a remainder of 1. Since
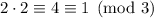 , we multiply the first term by 2.
, we multiply the first term by 2.
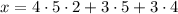
- Taken mod 4, the first and last terms vanish, and
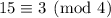 . Multiply by the inverse of 3 modulo 4 (which is 3 because
. Multiply by the inverse of 3 modulo 4 (which is 3 because
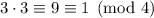 ), then by 2 to ensure the proper remainder is left.
), then by 2 to ensure the proper remainder is left.
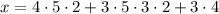
- Taken mod 5, the first two terms vanish, and
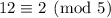 . Multiply by the inverse of 2 modulo 5 (3, since
. Multiply by the inverse of 2 modulo 5 (3, since
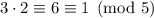 ) and again by 3.
) and again by 3.
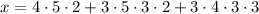
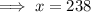
By the CRT, we have
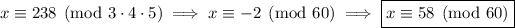
i.e. any number
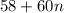 (where
(where
 is an integer) satisifes the system.
is an integer) satisifes the system.
b. The moduli are not coprime, so we need to check for possible contradictions. If
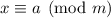 and
and
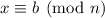 , then we need to have
, then we need to have
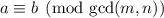 . This basically amounts to checking that if
. This basically amounts to checking that if
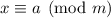 , then we should also have
, then we should also have
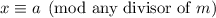 .
.

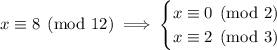
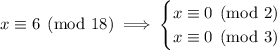
The last congruence conflicts with the previous one modulo 3, so there is no solution to this system.