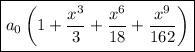We're looking for a solution of the form
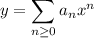
with derivative
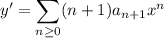
Note that
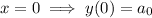 .
.
Substituting into the ODE gives

The first series starts with a constant term, while the second starts with a quadratic term, so we should pull out the first two terms of the first series and have it start at
 , then shift the index on the second series to achieve the same effect, which allows us to condense the left side as
, then shift the index on the second series to achieve the same effect, which allows us to condense the left side as
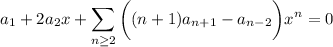
so that the series solution's coefficients are given according to the recurrence

We can simplify the latter equation somewhat to get it in terms of
 :
:
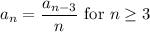
This shows dependency between coefficients that are 3 indices apart, so we check 3 cases:
- If
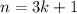 , where
, where
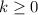 is an integer, then
is an integer, then

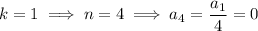
and so on for all such
 , giving
, giving

- If
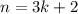 , then
, then

and we get the same conclusion as before,
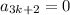
- If
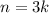 , then
, then
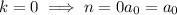
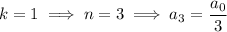
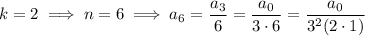
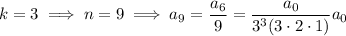
and so on, with the general pattern
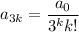
Then the series solution is
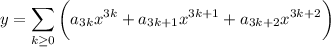
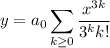
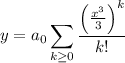
whose first four terms are