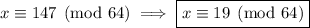Solve the following equations: (a) x^11=13 mod 35 (b) x^5=3 mod 64

Solve the following equations: (a) x^11=13 mod 35 (b) x^5=3 mod 64

asked Feb 5, 2020 39.8k views

1 Answer

a.

$x^(11)=13\pmod{35}\implies\begin{cases}x^(11)\equiv13\equiv3\pmod5\\x^(11)\equiv13\equiv6\pmod7\end{cases}$

By Fermat's little theorem, we have

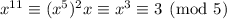
$x^(11)\equiv (x^5)^2x\equiv x^3\equiv3\pmod5$

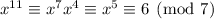
$x^(11)\equiv x^7x^4\equiv x^5\equiv6\pmod 7$

5 and 7 are both prime, so
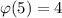$\varphi(5)=4$ and
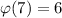$\varphi(7)=6$ . By Euler's theorem, we get

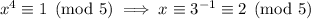
$x^4\equiv1\pmod5\implies x\equiv3^(-1)\equiv2\pmod5$

$x^6\equiv1\pmod7\impleis x\equiv6^(-1)\equiv6\pmod7$

Now we can use the Chinese remainder theorem to solve for
. Start with

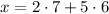
$x=2\cdot7+5\cdot6$

Taken mod 5, the second term vanishes and
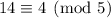$14\equiv4\pmod5$ . Multiply by the inverse of 4 mod 5 (4), then by 2.

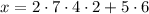
$x=2\cdot7\cdot4\cdot2+5\cdot6$

Taken mod 7, the first term vanishes and
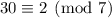$30\equiv2\pmod7$ . Multiply by the inverse of 2 mod 7 (4), then by 6.

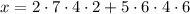
$x=2\cdot7\cdot4\cdot2+5\cdot6\cdot4\cdot6$

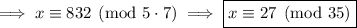
$\implies x\equiv832\pmod{5\cdot7}\implies\boxed{x\equiv27\pmod{35}}$

b.

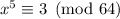
$x^5\equiv3\pmod{64}$

We have
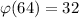$\varphi(64)=32$ , so by Euler's theorem,

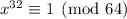
$x^(32)\equiv1\pmod{64}$

Now, raising both sides of the original congruence to the power of 6 gives

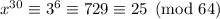
$x^(30)\equiv3^6\equiv729\equiv25\pmod{64}$

Then multiplying both sides by
x^2 gives

$x^(32)\equiv25x^2\equiv1\pmod{64}$

so that
x^2 is the inverse of 25 mod 64. To find this inverse, solve for
in
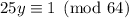$25y\equiv1\pmod{64}$ . Using the Euclidean algorithm, we have

64 = 2*25 + 14

25 = 1*14 + 11

14 = 1*11 + 3

11 = 3*3 + 2

3 = 1*2 + 1

=> 1 = 9*64 - 23*25

so that
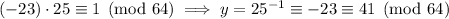$(-23)\cdot25\equiv1\pmod{64}\implies y=25^(-1)\equiv-23\equiv41\pmod{64}$ .

So we know

$25x^2\equiv1\pmod{64}\implies x^2\equiv41\pmod{64}$

Squaring both sides of this gives

$x^4\equiv1681\equiv17\pmod{64}$

and multiplying both sides by
tells us

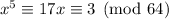
$x^5\equiv17x\equiv3\pmod{64}$

Use the Euclidean algorithm to solve for
.

64 = 3*17 + 13

17 = 1*13 + 4

13 = 3*4 + 1

=> 1 = 4*64 - 15*17

so that
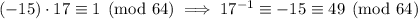$(-15)\cdot17\equiv1\pmod{64}\implies17^(-1)\equiv-15\equiv49\pmod{64}$ , and so
$x\equiv147\pmod{64}\implies\boxed{x\equiv19\pmod{64}}$

Randombits answered Feb 11, 2020

8.0k points

← Prev Question Next Question →

Search Qammunity.org