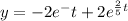Question

Solve 5y'' + 3y' – 2y = 0, y(0) = 0, y'(O) = 2.8 y(t) =( Preview

Answer 1

`y=(4)/(5)e^(t)-(4)/(5)e^{-(2)/(5)t}`

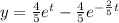
Explanation:

The given equation 5y'' + 3y' - 2y =0 can be written as

`(5D^(2)+3D-2)y(t)=0`

Solving for complementary function we have Roots of
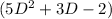`(5D^(2)+3D-2)` as follows

`(5D^(2)+5D-2D-2)`

`5D(D+1)-2(D+1)=0\\\\(5D-2)(D+1)=0\\\\\therefore D=-1\\D=+2/5`

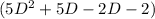
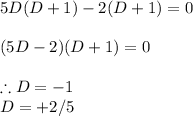
Thus the complementary function becomes

y=
`y=c_(1)e^{m_(1)t}+c_(2)e^{m_(2)t}`

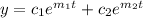
where

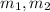`m_(1),m_(2)` are calculated roots

thus solution becomes

`y=c_(1)e^(-t)+c_(2)e^{(2)/(5)t}`

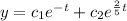
Now to solve for the coefficients we use the given boundary conditions

`y(0)=0\\\\\therefore c_(1)+c_(2)=0\\\\y'(0)=-c_(1)+(2)/(5)c_(2)=2.8\\\\\therefore c_(2)+(2)/(5)c_(2)=2.8\\\\c_(2)=2\\\\\therefore c_(1)=-2}`

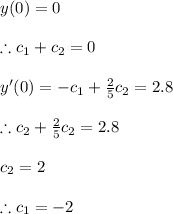
hence the solution becomes

`y=-2e^-{t}+2e^{(2)/(5)t}`