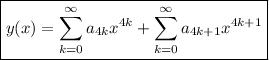Question

Solve this differential Equation by using power series
y''-x^2y=o

Answer 1

We're looking for a solution

`y=\displaystyle\sum_(n=0)^\infty a_nx^n`

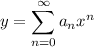
which has second derivative

`y''=\displaystyle\sum_(n=2)^\infty n(n-1)a_nx^(n-2)=\sum_(n=0)^\infty(n+2)(n+1)a_(n+2)x^n`

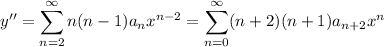
Substituting these into the ODE gives

`\displaystyle\sum_(n=0)^\infty(n+2)(n+1)a_(n+2)x^n-\sum_(n=0)^\infty a_nx^(n+2)=0`

`\displaystyle\sum_(n=0)^\infty(n+2)(n+1)a_(n+2)x^n-\sum_(n=2)^\infty a_(n-2)x^n=0`

`\displaystyle2a_2+6a_3x+\sum_(n=2)^\infty(n+2)(n+1)a_(n+2)x^n-\sum_(n=2)^\infty a_(n-2)x^n=0`

`\displaystyle2a_2+6a_3x+\sum_(n=2)^\infty\bigg((n+2)(n+1)a_(n+2)-a_(n-2)\bigg)x^n=0`

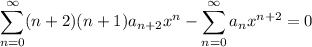
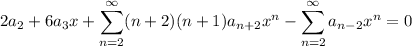
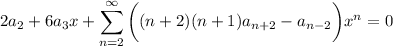
Right away we see
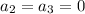`a_2=a_3=0`, and the coefficients are given according to the recurrence

`\begin{cases}a_0=y(0)\\a_1=y'(0)\\a_2=0\\a_3=0\\n(n-1)a_n=a_(n-4)&\text{for }n\ge4\end{cases}`

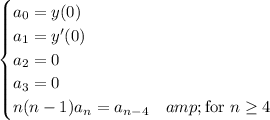
There's a dependency between terms in the sequence that are 4 indices apart, so we consider 4 different cases.

• If
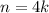  `n=4k`, where
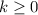  `k\ge0` is an integer, then

`k=0\implies n=0\implies a_0=a_0`

`k=1\implies n=4\implies a_4=(a_0)/(4\cdot3)=\frac2{4!}a_0`

`k=2\implies n=8\implies a_8=(a_4)/(8\cdot7)=(6\cdot5\cdot2)/(8!)a_0`

`k=3\implies n=12\implies a_(12)=(a_8)/(12\cdot11)=(10\cdot9\cdot6\cdot5\cdot2)/(12!)a_0`

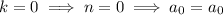
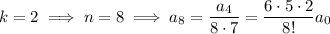
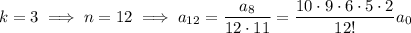
and so on, with the general pattern

`a_(4k)=(a_0)/((4k)!)\displaystyle\prod_(i=1)^k(4i-2)(4i-3)`

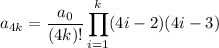
• If
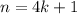  `n=4k+1`, then

`k=0\implies n=1\implies a_1=a_1`

`k=1\implies n=5\implies a_5=(a_1)/(5\cdot4)=(3\cdot2)/(5!)a_1`

`k=2\implies n=9\implies a_9=(a_5)/(9\cdot8)=(7\cdot6\cdot3\cdot2)/(9!)a_1`

`k=3\implies n=13\implies a_(13)=(a_9)/(13\cdot12)=(11\cdot10\cdot7\cdot6\cdot3\cdot2)/(13!)a_1`

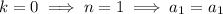
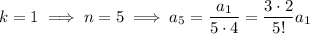
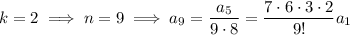
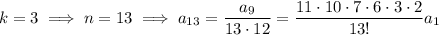
and so on, with

`a_(4k+1)=(a_1)/((4k+1)!)\displaystyle\prod_(i=1)^k(4i-1)(4i-2)`

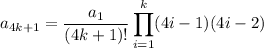
• If
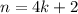  `n=4k+2` or
  `n=4k+3`, then

`a_2=0\implies a_6=a_(10)=\cdots=a_(4k+2)=0`

`a_3=0\implies a_7=a_(11)=\cdots=a_(4k+3)=0`

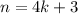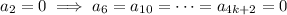
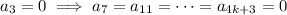
Then the solution to this ODE is

`\boxed{y(x)=\displaystyle\sum_(k=0)^\infty a_(4k)x^(4k)+\sum_(k=0)^\infty a_(4k+1)x^(4k+1)}`