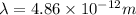Question

In a particular case of Compton scattering, a photon collides with a free electron and scatters backwards. The wavelength after the collision is exactly double the wavelength before the collision. What is the wavelength of the incident photon?

Answer 1

hence initial wavelength is
`\lambda =4.86*10^(-12)m`

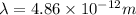
Step-by-step explanation:

shift in wavelength due to compton effect is given by

`\lambda ^(')-\lambda =(h)/(m_(e)c)*(1-cos\theta )`

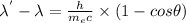
λ' = the wavelength after scattering

λ= initial wave length

h= planks constant

m_{e}= electron rest mass

c= speed of light

θ= scattering angle = 180°

compton wavelength is

`(h)/(m_(e)c)= 2.43*10^(-12)m`

`\lambda '-\lambda =2.43*10^(-12)*(1-cos\theta )`

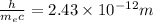
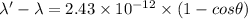
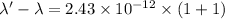`\lambda '-\lambda =2.43*10^(-12)*(1+1 )` ( put cos 180°=-1)

also given λ'=2λ

putting values and solving we get

`\lambda =4.86*10^(-12)m`

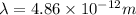
hence initial wavelength is
`\lambda =4.86*10^(-12)m`