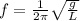Question

Show that the oscillation of a physical pendulum under small angle approximation is an simple harmonic motion. Find the oscillation frequency in terms of the pendulum parameters.

Answer 1

`f = (1)/(2\pi )\sqrt{(g)/(L)}`

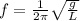
Step-by-step explanation:

Let the mass of bob in the simple pendulum is m and the effective length of the pendulum is L.

The value of acceleration due to gravity is g.

Let the pendulum is tilted by a small angle θ from the vertical.

The component of force which restore its position is given by

F = - m g Sinθ

(negative sign shows the opposite direction of displacement and the force)

If angle θ is small, then Sinθ = θ

F = - m g θ

According to diagram, θ = s / L

So, F = - m g s / L

Acceleration, a = F / m

a = - g x / L

As a ∝ - s

So, it is Simple harmonic motion.

Compare by A = - ω² s

Here,

ω² = g / L

We know that, ω = 2 Π f, where f is the frequency of oscillations.

So,

4 π²f² = g / L

`f = (1)/(2\pi )\sqrt{(g)/(L)}`