Question

Solve by the elimination method. Also determine whether the system is consistent or inconsistent and whether the equations are dependent or independent.

2x-8y=10

3x-12y=15

Please circle the answers.

Answer 1

The provided system of equation is consistent and the equations are dependent.

Explanation:

Consider the provided system of equations.

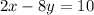`2x-8y=10`......(1)

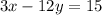`3x-12y=15`......(2)

Solve the above equations by elimination method.

Multiply the first equation by 3 and second equation by 2.

`6x-24y=30`

`6x-24y=30`

_________________

`0=0`

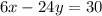
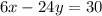
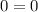
Which is true,

This means that the solution to the system of equation is all real numbers. Therefore, the equation have an infinite number of solutions.

If a system of the equation has one or infinite solution then it is known as a consistent system otherwise it is known as inconsistent.

The above equation has an infinite number of solutions, so the provided equations are consistent.

If a consistent system of the equation has only 1 solution, then it is known as an independent . If a consistent system of the equation has infinitely many solutions, then it is known as a dependent .

As the provided system of the equation has infinitely many solutions, so it is a dependent equation.

Hence, the provided system of equation is consistent and the equations are dependent.