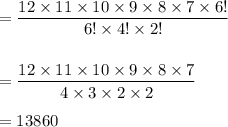Question

Sally has 6 red​ flags, 4 green​ flags, and 2 white flags. How many 12​-flag signals can she run up a flag​ pole? She can create nothing signals.

Answer 1

Hence, the answer is:

13860

Explanation:

Sally has 6 red​ flags, 4 green​ flags, and 2 white flags.

i.e. there are a total of 12 flags.

Now, we are asked to find the different number of arrangements that may be made with the help of these 12-flags.

We need to use the method of permutation in order to find the different number of arrangements.

The rule is used as follows:

If we need to arrange n items such that there are
`n_1` number of items of one type,
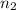`n_2` items same of other type .

Then the number of ways of arranging them is:

`=(n!)/(n_1!\cdot n_2!)`

Hence, here the number of ways of forming a flag signal is:

`=(12!)/(6!* 4!* 2!)`

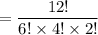
( since 6 flags are of same color i.e. red , 4 flags are of green color and 2 are of white colors )

`=(12* 11* 10* 9* 8* 7* 6!)/(6!* 4!* 2!)\\\\\\=(12* 11* 10* 9* 8* 7)/(4* 3* 2* 2)\\\\=13860`