Question

Show that 1n^ 3 + 2n + 3n ^2 is divisible by 2 and 3 for all positive integers n.

Answer 1

Prove:

Using mathemetical induction:

P(n) =
`n^(3)+2n+3n^(2)`

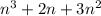
for n=1

P(n) =
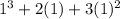`1^(3)+2(1)+3(1)^(2)` = 6

It is divisible by 2 and 3

Now, for n=k,
`n > 0`

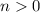
P(k) =
`k^(3)+2k+3k^(2)`

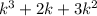
Assuming P(k) is divisible by 2 and 3:

Now, for n=k+1:

P(k+1) =
`(k+1)^(3)+2(k+1)+3(k+1)^(2)`

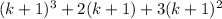
P(k+1) =
`k^(3)+3k^(2)+3k+1+2k+2+3k^(2)+6k+3`

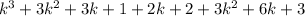
P(k+1) =
`P(k)+3(k^(2)+3k+2)`

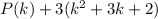
Since, we assumed that P(k) is divisible by 2 and 3, therefore, P(k+1) is also

divisible by 2 and 3.

Hence, by mathematical induction, P(n) =
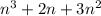`n^(3)+2n+3n^(2)` is divisible by 2 and 3 for all positive integer n.