Question

prove that if f is integrable on [a,b] and c is an element of [a,b], then changing the value of f at c does not change the fact that f is integrable or the value of its integral on [a,b]

Answer 1

Answer with Step-by-step explanation:

We are given that if f is integrable on [a,b].

c is an element which lie in the interval [a,b]

We have to prove that when we change the value of f at c then the value of f does not change on interval [a,b].

We know that limit property of an integral

`\int_(a)^(b)f dt=\int_(a)^(c)fdt+\int_(c)^(b) fdt`

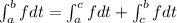
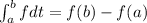`\int_(a)^(b) fdt=f(b)-f(a)`....(Equation I)

Using above property of integral then we get

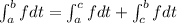`\int_(a)^(b)fdt=\int_(a)^(c)fdt+\int_(c)^(b) fdt`......(Equation II)

Substitute equation I and equation II are equal

Then we get

`\int_(a)^(b)fdt= f(c)-f(a)+{f(b)-f(c)}`

`\int_(a)^(b)fdt=f(c)-f(a)+f(b)-f(c)=f(b)-f(a)`

`\int_(a)^(c)fdt+\int_(c)^(b)fdt=f(b)-f(a)`

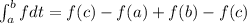
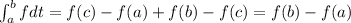
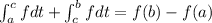
Therefore,
`\int_(a)^(b)fdt=\int_(a)^(c)fdt+\int_(c)^(b)fdt`.

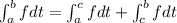Hence, the value of function does not change after changing the value of function at c.