Answer:
5.865 μs
Step-by-step explanation:
t₀ = Time taken to decay a muon = 2.20 μs
c = Speed of Light in vacuum = 3×10⁸ m/s
v = Velocity of muon = 0.927 c
t = Lifetime observed
Time dilation
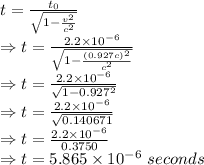
∴Lifetime observed for muons approaching at 0.927 the speed of light is 5.865 μs