Question

At noon, ship A is 50 nautical miles due west of ship B. Ship A is sailing west at 22 knots and ship B is sailing north at 23 knots. How fast (in knots) is the distance between the ships changing at 3 PM? (Note: 1 knot is a speed of 1 nautical mile per hour.)

Answer 1

30.66 knots

Step-by-step explanation:

Distance of ship A from B at noon = 50 NM

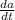`(da)/(dt)` = Velocity of ship A = 22 knots = 22 NM/h

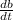`(db)/(dt)` = Velocity of ship B = 23 knots = 23 NM/h

Distance travelled by ship A from noon to 3 PM = 22×3 = 66 NM

a = Total distance travelled by ship A = 50+66 = 116 NM

b = Total distance travelled by ship B till 3 PM = 23×3 = 69 NM

c = Distance between Ship A and B at 3 PM = √(116²+69²) = 134.97 NM

a²+b² = c² (Pythagoras theorem)

Now differentiating with respect to time

`2a(da)/(dt)+2b(db)/(dt)=2c(dc)/(dt)\\\Rightarrow a(da)/(dt)+b(db)/(dt)=c(dc)/(dt)\\\Rightarrow (116* 22+69* 23)/(134.97)=(dc)/(dt)\\\Rightarrow (dc)/(dt)=30.66\ NM/h`

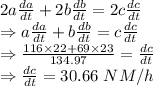
∴ The velocity with which the distance is changing at 3 PM (3 hours later) is 30.66 knots