Question

Prove the following by induction. In each case, n is apositive integer.

2^n ≤ 2^n+1 - 2^n-1 -1.

Answer 1

We rewrite the inequality as follows:

`2^n \leq 2^(n+1) - 2^(n-1) - 1\\1 \leq 2^(n+1) - 2^(n) - 2^(n-1)\\1 \leq 4\cdot 2^(n-2) - 2 \cdot 2^(n-1) - 2^(n-1)\\1 \leq (4-2-1) \cdot 2^(n-2)\\1 \leq 2^(n-2)`

Which is true because n was given to be a positive integer.

Answer 2

Answer with explanation:

We are asked to prove by the method of mathematical induction that:

`2^n\leq 2^(n+1)-2^(n-1)-1`

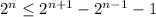
where n is a positive integer.

• Let us take n=1

then we have:

`2^1\leq 2^(1+1)-2^(1-1)-1\\\\i.e.\\\\2\leq 2^2-2^(0)-1\\\\i.e.\\2\leq 4-1-1\\\\i.e.\\\\2\leq 4-2\\\\i.e.\\\\2\leq 2`

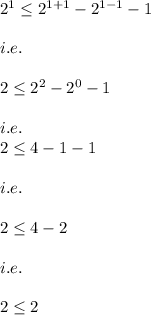
Hence, the result is true for n=1.

• Let us assume that the result is true for n=k

i.e.

`2^k\leq 2^(k+1)-2^(k-1)-1`

• Now, we have to prove the result for n=k+1

i.e.

To prove:
`2^(k+1)\leq 2^((k+1)+1)-2^((k+1)-1)-1`

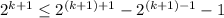
Let us take n=k+1

Hence, we have:

`2^(k+1)=2^k\cdot 2\\\\i.e.\\\\2^(k+1)\leq 2\cdot (2^(k+1)-2^(k-1)-1)`

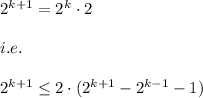
( Since, the result was true for n=k )

Hence, we have:

`2^(k+1)\leq 2^(k+1)\cdot 2-2^(k-1)\cdot 2-2\cdot 1\\\\i.e.\\\\2^(k+1)\leq 2^((k+1)+1)-2^(k-1+1)-2\\\\i.e.\\\\2^(k+1)\leq 2^((k+1)+1)-2^((k+1)-1)-2`

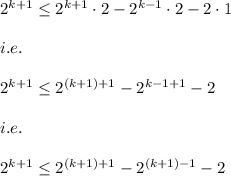
Also, we know that:

`-2<-1\\\\i.e.\\\\2^((k+1)+1)-2^((k+1)-1)-2<2^((k+1)+1)-2^((k+1)-1)-1`

(

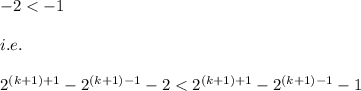
Since, for n=k+1 being a positive integer we have:

`2^((k+1)+1)-2^((k+1)-1)>0` )

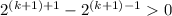Hence, we have finally,

`2^(k+1)\leq 2^((k+1)+1)-2^((k+1)-1)-1`

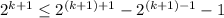
Hence, the result holds true for n=k+1

Hence, we may infer that the result is true for all n belonging to positive integer.

i.e.

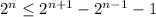`2^n\leq 2^(n+1)-2^(n-1)-1` where n is a positive integer.