Question

Photons with wavelength 1 pm are incident on electrons. What is the frequency of the Compton-scattered photons at an angle of 60°?

Answer 1

f = 1.354*10^{20} Hz

Step-by-step explanation:

By conservation of linear momentum, wavelength shift due to collision of photon to electron is given by following formula

`\lambda ^(')-\lambda =(h)/(m_(o)c)(1-cos\theta )`

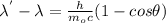
where h is plank constant = 6.626*10^{-34}

c = speed of light = 3*10^{8} m/s

scattered angle = 60 degree

m = rest mass of electron = 9*10^{-31}

`\lambda ^(')=10^(-12) +(6.626*10^(-34))/(9*10^(-31)*3*10^(8))(1-cos60^(o) )`

`\lambda ^(')= 2.215 pm`

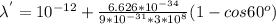
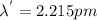
we know that 1 pm = 10^{-12}m

`f = (c)/(\lambda ^('))`

`f = (3*10^(8))/(2.215 *10^(-12)) = 1.354*10^(20) Hz`

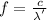
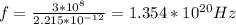
f = 1.354*10^{20} Hz