Answer with Step-by-step explanation:
We are given that A, B and C are subsets of universal set U.
We have to prove that

Proof:
Let x
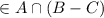
Then
 and
and
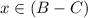
When
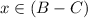 then
then
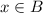 but
but
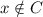
Therefore,
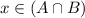 but
but

Hence, it is true.
Conversely , Let
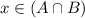 but
but
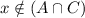
Then
 and
and
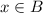
When
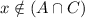 then
then
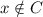
Therefor,
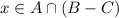
Hence, the statement is true.