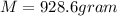Question

Please do parts (a) and part (b) below and include diagrams where applicable:

A mass m at the end of a spring vibrates with a frequency of 0.90 Hz. When an additional 520-g mass is added to m, the frequency is 0.50 Hz.

a) What is the value of m?

b) Calculate the total mass needed for the system to vibrate with a freq. of 0.45 Hz.

Answer 1

Part a)

m = 232.1 gram

Part b)

M = 928.6 gram

Step-by-step explanation:

Part a)

As we know that frequency of vibration for a given spring block system is given by formula

`f = (1)/(2\pi)\sqrt{(k)/(m)}`

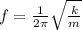
so if it is given as 0.90 Hz then we will have

`0.90Hz = (1)/(2\pi)\sqrt{(k)/(m)}`

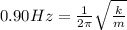
Now if additional mass is attached with it the frequency changed to 0.50 Hz

`0.50 Hz = (1)/(2\pi)\sqrt{(k)/(m + 520)}`

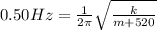
now divide two equations

`(0.90)/(0.50) = \sqrt{(m + 520)/(m)}`

`3.24m = m + 520`

`m = 232.1 g`

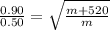
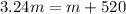
Part b)

Now the frequency is changed to 0.45 Hz

so again we will have

`0.45 Hz = (1)/(2\pi)\sqrt{(k)/(M)}`

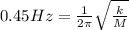
again divide it with first equation above

`(0.90)/(0.45) = \sqrt{(M)/(m)}`

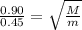
as we know that m = 232.1 g

so total mass needed for 0.45 Hz will be

`M = 928.6 gram`