Question

Please solve in [0,2π] or [0°,360°]

A.) Cos^2 x+2 cos x=3

B.) 2 sin^2 0+7 sin 0=4

C.) tan^2 x+4= 2sec^2 x+tan x

Answer 1

Answer with explanation:

The equation using trigonometric function are whose value we have to evaluate in the interval [0, 2π].

1.→

cos²x +2 cos x=3

→cos²x +2 cos x-3=0

→cos²x +3 cos x-cos x-3=0

→cos x ( cos x +3) -1×(cos x +3)=0

→ (cos x -1)(cos x +3)=0

→cos x -1= 0 ∧ →cos x+3=0

→cos x =1 ∧ → cos x = -3

⇒-1 ≤ cos x ≤ 1

→cos x=1

`\cos x=\cos 0^(\circ)\\\\x=2 n\pi \pm 0^(\circ)\\\\x=2 n\pi`

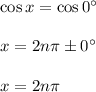
where, n is any integer.

→Solution in the Interval [0, 2π] is , x=0, 2 π

2.

2 sin² Ф +7 sin Ф =4

→2 sin² Ф +7 sin Ф -4=0

→2 sin² Ф +8 sin Ф- sin Ф -4=0

→2 sin Ф × (sin Ф +4) -1 × (sin Ф +4)=0

→ (2 sin Ф -1)(sin Ф +4)=0

→ 2 sin Ф -1=0 ∧ →sin Ф +4=0

→sin Ф ≠ -4≡→ ∵ -1 ≤ sin Ф ≤ 1

`\rightarrow \sin \Phi =(1)/(2)\\\\\rightarrow\sin \Phi =\sin ((\pi)/(6))\\\\ \rightarrow\Phi=n\pi +(-1)^n(\pi)/(6)\\\\\rightarrow \Phi=(\pi)/(6),(5\pi)/(6)`

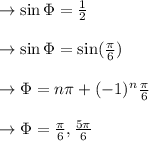
Where , n is any Integer.

3.

→tan² x+4=2 sec² x+tan x

→tan² x+4=2(1+tan²x)+tan x

→2 tan²x -tan²x +tan x +2-4=0

→tan²x +tan x -2=0

→tan²x +2 tan x -tan x -2=0

→tan x (tan x +2) -1×(tan x +2)=0

→(tan x-1)(tan x +2)=0

→tan x-1 =0 ∧ tan x +2=0

→tan x=1 ∧ tan x = -2

→tan x=1

`\rightarrow \tan x=\tan ((\pi)/(4))\\\\x=n\pi+ (\pi)/(4)\\\\x=(\pi)/(4),(5\pi)/(4)`

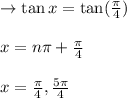
→tan x= -2

`\rightarrow \tan x=2\\\\\rightarrow x=k\pi+ tan^(-1)2\\\\\rightarrow x=tan^(-1)2, \pi +tan^(-1)2`

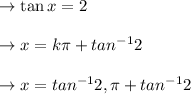
where, k and n are integer.