Answer:
Below.
Explanation:
To prove this for mathematical induction, we will need to prove:
Part 1) That
 is a multiple of 6 for n=1.
is a multiple of 6 for n=1.
Part 2) That, if by assuming
 is a multiple of 6, then showing
is a multiple of 6, then showing
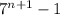 is a multiple of 6.
is a multiple of 6.
----------------------------------------------------------------------------------------------
Part 1) If n=1, we have
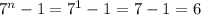 where 6 is a multiple of 6 since 6 times 1 is 6.
where 6 is a multiple of 6 since 6 times 1 is 6.
Part 2) A multiple of 6 is the product of 6 and k where k is an integer. So let's assume that there is a value k such that
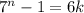 for some number natural number
for some number natural number
 .
.
We want to show that
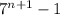 is a multiple of 6.
is a multiple of 6.
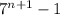
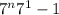


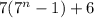
 (this is where I applied my assumption)
(this is where I applied my assumption)
![6[7k+1]](https://img.qammunity.org/2020/formulas/mathematics/college/fnqvc1j4vmtr7ypy4giqbwehyjgm9b4rmt.png) (factoring with the distributive property)
(factoring with the distributive property)
Since 7k+1 is an integer then 6(7k+1) means that
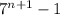 is a multiple of 6.
is a multiple of 6.
This proves that
 is a multiple of 6 for all natural n.
is a multiple of 6 for all natural n.