Question

Please determine whether the set S = x^2 + 3x + 1, 2x^2 + x - 1, 4.c is a basis for P2. Please explain and show all work. It is fine to use technology.

Answer 1

The vectors in
`S` form a basis of
`P_2` if they are mutually linearly independent and span
`P_2`.

To check for independence, we can compute the Wronskian determinant:

`\begin{vmatrix}x^2+3x+1&2x^2+x-1&4\\2x+3&4x+1&0\\2&4&0\end{vmatrix}=4\begin{vmatrix}2x+3&4x+1\\2&4\end{vmatrix}=40\\eq0`

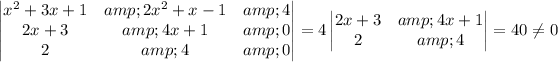
The determinant is non-zero, so the vectors are indeed independent.

To check if they span
`P_2`, you need to show that any vector in
`P_2` can be expressed as a linear combination of the vectors in
`S`. We can write an arbitrary vector in
`P_2` as

`p=ax^2+bx+c`

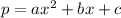
Then we need to show that there is always some choice of scalars
`k_1,k_2,k_3` such that

`k_1(x^2+3x+1)+k_2(2x^2+x-1)+k_34=p`

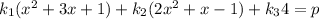
This is equivalent to solving

`(k_1+2k_2)x^2+(3k_1+k_2)x+(k_1-k_2+4k_3)=ax^2+bx+c`

or the system (in matrix form)

`\begin{bmatrix}1&1&0\\3&1&0\\1&-1&4\end{bmatrix}\begin{bmatrix}k_1\\k_2\\k_3\end{bmatrix}=\begin{bmatrix}a\\b\\c\end{bmatrix}`

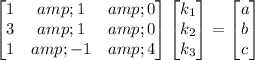
This has a solution if the coefficient matrix on the left is invertible. It is, because

`\begin{vmatrix}1&1&0\\3&1&0\\1&-1&4\end{vmatrix}=4\begin{vmatrix}1&2\\3&1\end{vmatrix}=-20\\eq0`

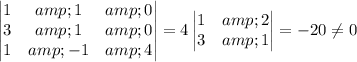
(that is, the coefficient matrix is not singular, so an inverse exists)

Compute the inverse any way you like; you should get

`\begin{bmatrix}1&1&0\\3&1&0\\1&-1&4\end{bmatrix}^(-1)=-\frac1{20}\begin{bmatrix}4&-8&0\\-12&4&0\\-4&3&-5\end{bmatrix}`

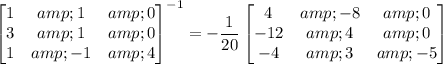
Then

`\begin{bmatrix}k_1\\k_2\\k_3\end{bmatrix}=\begin{bmatrix}1&1&0\\3&1&0\\1&-1&4\end{bmatrix}^(-1)\begin{bmatrix}a\\b\\c\end{bmatrix}`

`\implies k_1=\frac{2b-a}5,k_2=\frac{3a-b}5,k_3=(4a-3b+5c)/(20)`

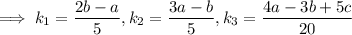
A solution exists for any choice of
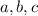`a,b,c`, so the vectors in
`S` indeed span
`P_2`.

The vectors in
`S` are independent and span
`P_2`, so
`S` forms a basis of
`P_2`.