Question

Problem 7. Show that among any four numbers one can find at least two numbers so that their difference is divisible by 3. las i visible mig any four

Answer 1

Explained

Explanation:

let there be
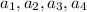`a_(1) , a_(2), a_(3), a_(4)` any four integers.

when dividing any integer by 3 there 3 remainders {0,1,2}

Now since there are 4 numbers and 3 integers certainly there be 2 numbers with same remainder when divided by 3.

that is there exist
`a_(i) and a_(j)`

`a_(i)=3m+r`

`a_(j)=3n+r`

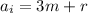
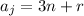
where m and n are integers and
`r\in{0,1,2}`

`a_(i)-a_(j)=3m+r-3n-r=3(m+n)`

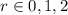
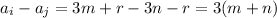
thus their difference is divisible by 3