Answer: 38
Explanation:
- If P and Q are two different set the their difference is given by P-Q i.e. the number of elements in P bit not Q .
i.e.
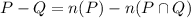
Let A be the number of students who correctly answered the first question and B be the number of students who correctly answered the second question .
Given :
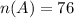
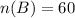
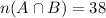
Then the number of students who answered the first question correctly, but not the second is given by :-

Hence, the number of students who answered the first question correctly, but not the second is 38.