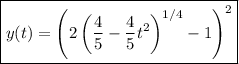1. I suppose the ODE is supposed to be

Solving for
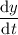 gives
gives
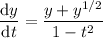
which is undefined when
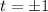 . The interval of validity depends on what your initial value is. In this case, it's
. The interval of validity depends on what your initial value is. In this case, it's
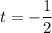 , so the largest interval on which a solution can exist is
, so the largest interval on which a solution can exist is
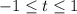 .
.
2. Separating the variables gives

Integrate both sides. On the left, we have
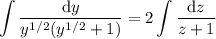
where we substituted
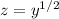 - or
- or
 - and
- and
 - or
- or
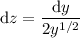 .
.
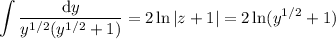
On the right, we have

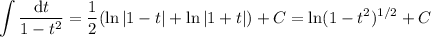
So
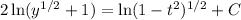
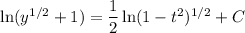
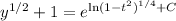
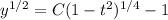
I'll leave the solution in this form for now to make solving for
 easier. Given that
easier. Given that
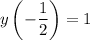 , we get
, we get
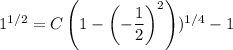
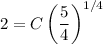
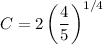
and so our solution is